I'm modifying a pair of ATC SCM20 Pro PSL Mk2 speakers - making them active and other things. I'm curious about it's included passive crossover though, because it's a 3rd order butterworth with no audible peak in the crossover region.
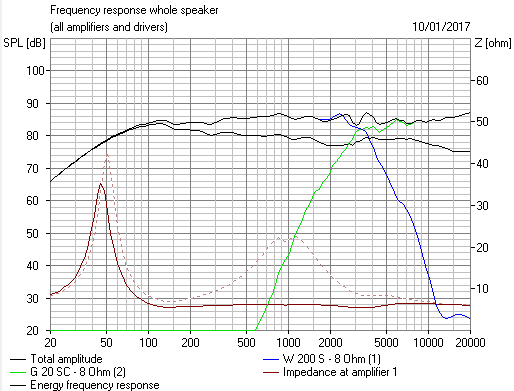
The advertised crossover point is 2.1khz, but when the woofer is disconnected on one side, tweeter on the other, the levels match instead at 1.975khz.
Is this a legitimate way to design, separating the crossovers so that the tweeter's -3db point is 2.1khz, and the woofer's -3db point is 1.85khz, with the -6db points for each 1.975khz to sum close to flat? I think it's what ATC did (haven't checked with a scope yet).
The only real problem I can think of from designing this way is maybe a bit of a wobble in the frequency response, realistically no more than 1db. The drivers could have as much variation, so not a problem in my eyes, as long as the high and low points aren't accentuated by either of the drivers' responses.
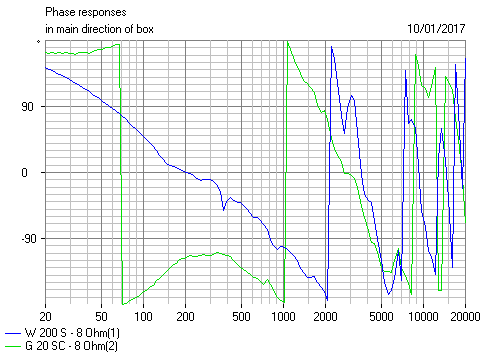
Would phase be audibly affected, or is this an ingenious way to get around the 3db peak normally associated with 3rd order butterworths?
I like the way it sounds, so I might emulate this configuration for my active design, although at a lower frequency
The advertised crossover point is 2.1khz, but when the woofer is disconnected on one side, tweeter on the other, the levels match instead at 1.975khz.
Is this a legitimate way to design, separating the crossovers so that the tweeter's -3db point is 2.1khz, and the woofer's -3db point is 1.85khz, with the -6db points for each 1.975khz to sum close to flat? I think it's what ATC did (haven't checked with a scope yet).
The only real problem I can think of from designing this way is maybe a bit of a wobble in the frequency response, realistically no more than 1db. The drivers could have as much variation, so not a problem in my eyes, as long as the high and low points aren't accentuated by either of the drivers' responses.
Would phase be audibly affected, or is this an ingenious way to get around the 3db peak normally associated with 3rd order butterworths?
I like the way it sounds, so I might emulate this configuration for my active design, although at a lower frequency
Electrically, but isn't there a 3db gain in efficiency from doubling the number of radiators?
Edit: don't other crossover types cross at -6db and sum to flat?
Edit: don't other crossover types cross at -6db and sum to flat?
Last edited:
Theoretically speaking.. there is a power dip with -6dB crossovers. Power is flat with the 3rd order butterworth, and so is axial response.
X-o's that sum flat are in phase at the x-o point. If they sum flat at -3dB is' because there is a 90 degree phase difference at the x-o point. Think of the amplitude as the two legs of a right triangle and the summed amplitude is the hypotenuse. A = sqrt (0.707^2 + 0.707^2) = 1.0
Also the included passive crossover might be 3rd order Butterworth electrical but when combined with the drives natural roll off things will look quite different.
I am sure John Kreskovsky knows more than most of us about all the different filter types and their phase characteristics. 🙂
But here's one that I think was BW3:
Joachim Gerhard's Sonics/Canalis Anima. The reviewer in stereophile didn't like the above axis lobing, so Joachim flipped the tweeter polarity for the Mk. II model. 😀
5" drivers are quite easy to work with for BW3, as are 8" drivers. 6", I am not to sure.
The BBC LS3/5A was a BW3 design IMO, but not time aligned, like this sort of Harbeth HL-P3 homage:
Flat power has a pleasant sound, 90 degree phase at crossover, -3dB cross. Energy frequency response is reasonably flat.
This more -6dB LR4 phase aligned:
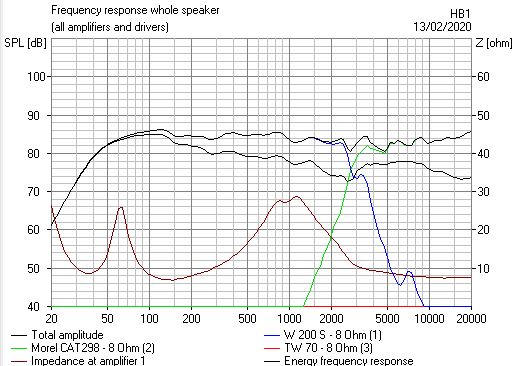
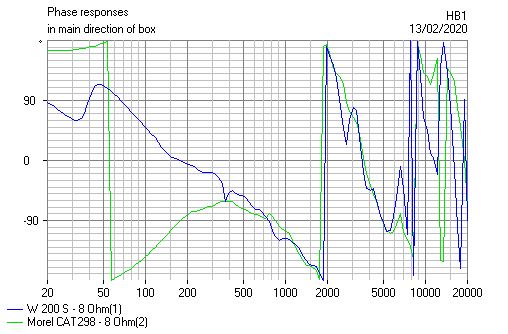
You can see the -3dB power hole in the second images.
Restoring Monitor Audio R300 bookshelf speakers.
But here's one that I think was BW3:
Joachim Gerhard's Sonics/Canalis Anima. The reviewer in stereophile didn't like the above axis lobing, so Joachim flipped the tweeter polarity for the Mk. II model. 😀
5" drivers are quite easy to work with for BW3, as are 8" drivers. 6", I am not to sure.
The BBC LS3/5A was a BW3 design IMO, but not time aligned, like this sort of Harbeth HL-P3 homage:
Flat power has a pleasant sound, 90 degree phase at crossover, -3dB cross. Energy frequency response is reasonably flat.
This more -6dB LR4 phase aligned:
You can see the -3dB power hole in the second images.
Restoring Monitor Audio R300 bookshelf speakers.
Last edited:
In reality a crossover is third order Butterworth only if the acoustic output of each of the drivers matches the slopes of a third order Butterworth filter. The electrical inputs to the drivers to achieve this result will not look anything like the slopes or fcs of a third order Butterworth filter!
A real loudspeaker is far from the pure resistive load needed to terminate a passive filter, regardless of order or shape. Loudspeaker drivers are typically designed to have a flat frequency response (or occasionally power response) with a constant voltage drive at their input terminals. To use with a passive crossover at the very least the driver needs a Zobel network to balance rising impedance with frequency and a conjugate RLC network to flatten the driver resonance bump so that the crossover is terminated quasi properly. This is before taking into account the fall off in response at either end of the driver's passband.
Finally, the only order of crossover that has a flat frequency response and power response is the first order. This is a consequence of physics, not how good the drivers, how clever the designer is, or whether the filter is Butterworth, Bessel, Linkwitz-Riley or Blind-freddy. Crossover filters of order two or higher do not recombine correctly to recreate the original signal wave-shape even electronically, let alone after adding imperfect drivers. A simple experiment is to recombine the outputs of an electronic crossover with selectable slopes and curves. It is quite obvious that anything other than first order changes the sound.
A real loudspeaker is far from the pure resistive load needed to terminate a passive filter, regardless of order or shape. Loudspeaker drivers are typically designed to have a flat frequency response (or occasionally power response) with a constant voltage drive at their input terminals. To use with a passive crossover at the very least the driver needs a Zobel network to balance rising impedance with frequency and a conjugate RLC network to flatten the driver resonance bump so that the crossover is terminated quasi properly. This is before taking into account the fall off in response at either end of the driver's passband.
Finally, the only order of crossover that has a flat frequency response and power response is the first order. This is a consequence of physics, not how good the drivers, how clever the designer is, or whether the filter is Butterworth, Bessel, Linkwitz-Riley or Blind-freddy. Crossover filters of order two or higher do not recombine correctly to recreate the original signal wave-shape even electronically, let alone after adding imperfect drivers. A simple experiment is to recombine the outputs of an electronic crossover with selectable slopes and curves. It is quite obvious that anything other than first order changes the sound.
Last I checked, 3rd order Butterworth sums flat and has a flat power response, assuming coincident drivers and flat frequency, impedance response. What it can't do is reproduce a square wave like 1st order can (assuming extremely rare and usually inapplicable conditions). But yes, as has been noted, a 3rd order electrical filter is not a synonym for 3rd order Butterworth.
Last edited:
Thank you for correcting me on Butterworth alignments, but in any case I don't consider high fidelity sound reproduction inapplicable conditions.
Of course a first order crossover, even when measured by the acoustic output of the drivers, does not guarantee fidelity as there are a lot of other issues involved. But what is lost in a higher than first order crossover can never be regained.
The biggest loss of higher order crossovers compared to first is in the interface between the loudspeaker and the room, IMHO. First order loudspeakers are much more room tolerant, and tolerant of the position of the speaker in the room and the position of the listener in the room.
The only way to know/experience the difference is to compare otherwise identical loudspeaker systems with first and higher order crossovers in the real world. Once you have, high order crossovers just sound wrong (because they are) and are relatively easily identified by their sound character.
If in doubt, listen to acoustic instruments acoustically, and then listen to how they sound reproduced by loudspeakers. The difference in sound caused by the crossover (whether passive or active makes no difference) of order higher than 1 is inarguable, unless one thinks that the sound of acoustic instruments listened to acoustically is wrong!
Last edited:
'Inapplicable conditions' refers to the vast majority of situations where 1st order filtering cannot reproduce a square-wave or linear phase. To do so typically requires specific physical geometry[ies] of drive units, baffles &c., and usually for the listener to be at one point in three dimensional space. The old Dunlavy & most current Duntech speakers are good examples, if you're seated correctly. But this simply isn't the case with many implementations, and often can't be for a variety of practical reasons.
How so? Granted, assuming flat frequency, impedance responses & coincident / time-aligned driver configuration, then it has a flat summed frequency & power response, but something like a linear-phase Dunlavy for e.g. is highly intolerant of listener position and off-axis summing usually runs into issues (unless the drivers happen to be coaxial). I'm afraid I don't quite see how this corrolates into greater tolerance of room acoustics & speaker / listener position. The latter as noted tends to be somewhat variable, and speaker position within a room acoustic tends to be dominated by room modes and the on / off axis response which is partly contrived by the filter, but also depends on the drive units & the LF alignment.
For the rest -I'll simply say that I respect your opinion, but disagree with the sweeping generalisation, because in many cases it simply isn't true, and leave it there, as this thread is about 3rd order filters and we don't wish to take it further off topic.
Last edited:
I see
This makes sense to me, and also explains the flat power response and different sonic character above and below axis (not a huge difference, but the one unique to BW3)
Not these speakers - The tweeter I've measured sans crossover, and it's flat for almost the entire octave below the xo- ~75hz short. So it's at least 15db down before its rolloff. The woofer through the crossover drops off at 18db/oct, but I'm sure by 4khz it's beaming so its power response is off. It's one of the reasons I'm modifying the speakers and lowering the crossover is for a better power response. It's not bad because it's a 5" cone to 1" dome at just under 2khz, but there's room for improvement
They look very similar to me... where exactly is the hole?
I think I remember doing this a long time ago. Do you recall which is next best?
I haven't compared the same drivers in the same enclosure with a first and then higher order crossover, but I have listened to a pair of totem speakers with a first order crossover hooked up to a 1.5" dome and 5" woofer. It did sound pretty good, but from what I remember they were more picky about the exact spot you were in. Outside of that spot though was better overall than the peakers with higher order crossovers. Though it could have been the set, I've only heard one.
I came across this a long time ago and completely forgot it existed! Thanks for sharing it. The second page is basically my use case and shows what can be gained (power response) by moving the crossover from 2 to 1.4khz. The only difference from my speaker being its woofer's cone is 5", not 6, in diameter. And I don't plan to go up to 7th order when lowering the crossover. I might though, if such a steep slope won't introduce audible artifacts.
In the 3rd order 2khz example it's said "woofer beaming" is creating the 3db dip centered at 1.7khz in the power response, but it is VC inductance attenuating the increasingly focused beam of sound, which would otherwise, with frequency, be increasing in amplitude.
In the 7th order 1.4khz example, the dip is narrower and shallower (1.5db).
With my 5 inch woofer crossed over at 1.4khz, I think I'll get almost as good a power response to the 7th order butterworth on a 6. But I plan to cross lower at 1.2khz, which should ensure I match it.
How much of a dip can there be in the power response with the design still considered to be ideal? I know, 0db lol. But realistically. I don't see power responses posted or advertised, so I don't know. Have popular speakers been measured by people online who have then made results available?
Last edited:
Thank you for the detailed reply, however it is not true that John Danlavy's are intolerant of listener position. Certainly the waveshape reconstruction is, but the way the room behaves is a function of the system power response, which is incredibly well controlled in Dunlavy's own designs (I have no knowledge of designs by subsequent engineers). The benefit of first order crossovers is the gentle way that performance "deteriorates" off axis compared to higher order crossovers, and of course that the crossover doesn't change the nature of the sound of real acoustic sources such as voices and instruments.
It's interesting that you mention Duntech, because John was gracious enough to explain his design approach to me and even allowed me to use his research facilities in Adelaide in the mid to late '80s to do development work on public address loudspeakers when I was the Sound Master at the Adelaide Festival Centre. John's work and 80s and 90s AES papers by another Adelaidian, David Murphy, using Spice modelling to model the polar response of coincident drivers, were pivotal in the beginning of my understanding of the loudspeaker room interface.
Later I had responsibility for workplace hearing protection, and learning in this role gave me further insight into the ear/brain auditory response mechanism and its interface with room acoustics, which added even more to my conviction about the deleterious effect of high order crossovers, especially for listeners with some NIHL or more correctly exposure induced hearing loss.
I was also fortunate enough to work in the late '90s with David Griesinger of Lexicon fame who explained much more about the perception of human hearing in relation to speech and music than I was able to understand, information which also reinforced the benefit of first order crossovers compared to higher order, when it comes to, for example, hear individual violins in an orchestra, or understand a voice with background noise, for example.
I think you might not have seen my question. Basically I wanted to know which order crossover sounds next best to first, only considering the sound quality of the recombined sums of the filtered source material (obviously through a pair of headphones lol).
What does it sound like? Are there certain types of sounds (taps, saw wave synthetic etc.) which are affected more?
You say higher order is bad. So does a 3rd sound worse than a 2nd, 4th worse than 3rd? Or is there a rule, like odds always sounds better than the even before them?
Even if the change in sound from the higher order filter is not easily identifiable in a speaker system, it is still always there. Minimizing it is something I'd like to do in future designs
I am not able to give a qualified opinion, either subjective or objective in response to your question. I now only designed speaker systems with first order crossovers for the reasons above. Occasionally I 'upgrade' systems with higher order crossovers to first order either for a significant benefit (e.g. a centre channel speaker where speech intelligibility is significantly enhanced, especially for listeners with some age or exposure induced hearing loss), or vintage speakers where the original crossovers were not well engineered or implemented (e.g. KEF B139 / B110 based systems and other systems of that vintage). I've also implemented first order crossovers for some of the newer Dynaudio systems introduced since its transfer to Chinese ownership. Under Wilfried Ehrenholz's ownership Dynaudios were almost exclusively first order designs.
In a general sense, one the the desired qualities of a speaker system is freedom from discontinuities in the power response, which needs to taper down over the audio passband nominally to mimic real audio sources like voices and instruments. Therefore if Butterworth filters of order greater than 1 have a flat power response they would satisfy this requirement. Whether using Butterworth for a particular design is more beneficial overall than another alignment I do not know or have an opinion on, although before I met John Dunlavy I exclusively designed hifi, PA and nightclub systems with 3rd order Butterworth filters. Since the '90s I have only used first orders in my own designs.
If you wish to explore the differences in sound quality of different crossover orders and alignments, a digital programable multi-way crossover is invaluable because you can switch rapidly between different designs. Also the active crossover implementation means that each driver is driven from an ideal voltage source, so you can make decisions based on an idealised crossover alignment without have to spend time developing Zobel and conjugate networks to get your drivers to terminate a passive crossover as best as possible.
For a professional speaker designer a digital programable active crossover is an invaluable tool and aid to rapid prototyping with one major caveat: it is not safe to assume that crossover implementation in any given product is actually correctly implemented in code, so it is necessary to verify that the digital crossover is actually doing what it is supposed to before making subjective evaluations. I have often discovered digital equalisers and crossovers with faulty algorithms, even from well respected manufacturers.
Of course in the real world a speaker system with a first order crossover and real drivers will not achieve true first order acoustic slopes, however by concentrating on the octave above and below crossover frequencies, and not getting too worried about what happens outside of that range (with the exception of resonances which must be addressed to a couple of octaves away from the crossover) I find pretty good real world results can be achieved.
I should be able to answer question of the change in sound character for individual instruments or sounds, but I have long since forgotten. Switch some headphones between the input to, and the summed outputs of, a digital crossover programmed to any filter shape of order 2 or higher and you will clearly hear the difference between input and output.
The last time I did this was in ~2004 when I was designing a nightclub system with active crossovers. I ended up using first order for sound quality, and making sure the systems were robust enough to achieve the necessary SPL with plenty of headroom.
The last time I did this was in ~2004 when I was designing a nightclub system with active crossovers. I ended up using first order for sound quality, and making sure the systems were robust enough to achieve the necessary SPL with plenty of headroom.
Dunlavy SC-1 as measured by John Atkinson, horizontal and vertical axis. As JA said -don't listen to this speaker standing up. 😉 As you would expect from a symmetric array on the vertical axis, with 1st order filtering. The larger models followed similar trends, detail varying with driver and implementation details.
John Dunlavy was an excellent designer and I doubt anybody would disagree with that. But he was obliged to work within the laws of physics. It is not disparaging to note that like everybody else, he picked his compromises according to his priorities (in his case, on-axis and phase response), did a damn good job within that context, and he was the first to note limitations / usage requirements, e.g. stressing minimum listening distances (and heights) for such products.
Attachments
Last edited: