I'm trying to figure out what the "peak" SPL capability of this combination of drivers is, in a sealed cabinet, the volume of which is optimised for the 12" (sub)woofer. The loudness capability of studio monitors is usually specified in terms of "peak" SPL @ 1m. The system will be tri-amplified with DSP... Hypex or equivalent.
The Satori TW29DN-B tweeter has a sensitivity of 96 dB (2.83 V / 1 m, 4 Ohm), can do 112 dB SPL @ 1m when fed with 80W. But this is per "IEC 268-5, high-pass Butterworth, 2600 Hz, 12 dB/oct". (For the sake of this situation, let us assume I have the said filter in place.)
The Faital Pro 6RS140 has a sensitivity of 93 dB (1W / 1m) and can handle 200W (2 Hours Test According to AES 2-1984 Rev. 2003) and 400W at "maximum power". ("Maximum power is defined as 3dB greater than nominal power.") This speaker will comfortably do 112 dB SPL when crossed over above 200 Hz, so it doesn't worry me.
The SB34NRX75-6 has a sensitivity of 90 dB (2.83V / 1m) and a "rated power handling of 200W. (IEC 268-5, T/S parameters measured on drive units that are broken in.) I am able to simulate a response of 106 dB SPL @ 1m with -3 dB point at ~32 Hz, before hitting x-max.
The SB Acoustics 12" woofer can deliver 106 dB SPL and the tweeter can do 112 dB SPL, but they comply with 'IEC 268-5' test standards, while the Faital mid-woofer complies with 'AES 2-1984 Rev. 2003'. As I said, the Faital is far too robust, so I'll ignore it for now.
I'm trying to figure out what IEC 268-5 means in this context. According to Wikipedia:
Now, by doubling the power to the 12" driver, I'm able to get a 3 dB boost in SPL, but the excursion goes to about 15mm... Xmax is 11mm and XLim (I think) is 17mm for this driver.
Two questions:
1) Looking at the 12" driver in isolation, is it fair to say that that it's "Peak SPL" is 109 dB @ 1m, while continuous SPL is 106 dB? (Excursion past 106 dB is > XMax but < Xlim).
2) What about the summing of the drivers? If the (sub)woofer and mid-woofer can each put out 106 dB continuous and 109 dB peaks, they should be able to put out 109 dB continuous and 112 dB peaks together...?
Thanks in advance,
The Satori TW29DN-B tweeter has a sensitivity of 96 dB (2.83 V / 1 m, 4 Ohm), can do 112 dB SPL @ 1m when fed with 80W. But this is per "IEC 268-5, high-pass Butterworth, 2600 Hz, 12 dB/oct". (For the sake of this situation, let us assume I have the said filter in place.)
The Faital Pro 6RS140 has a sensitivity of 93 dB (1W / 1m) and can handle 200W (2 Hours Test According to AES 2-1984 Rev. 2003) and 400W at "maximum power". ("Maximum power is defined as 3dB greater than nominal power.") This speaker will comfortably do 112 dB SPL when crossed over above 200 Hz, so it doesn't worry me.
The SB34NRX75-6 has a sensitivity of 90 dB (2.83V / 1m) and a "rated power handling of 200W. (IEC 268-5, T/S parameters measured on drive units that are broken in.) I am able to simulate a response of 106 dB SPL @ 1m with -3 dB point at ~32 Hz, before hitting x-max.
The SB Acoustics 12" woofer can deliver 106 dB SPL and the tweeter can do 112 dB SPL, but they comply with 'IEC 268-5' test standards, while the Faital mid-woofer complies with 'AES 2-1984 Rev. 2003'. As I said, the Faital is far too robust, so I'll ignore it for now.
I'm trying to figure out what IEC 268-5 means in this context. According to Wikipedia:
Now, by doubling the power to the 12" driver, I'm able to get a 3 dB boost in SPL, but the excursion goes to about 15mm... Xmax is 11mm and XLim (I think) is 17mm for this driver.
Two questions:
1) Looking at the 12" driver in isolation, is it fair to say that that it's "Peak SPL" is 109 dB @ 1m, while continuous SPL is 106 dB? (Excursion past 106 dB is > XMax but < Xlim).
2) What about the summing of the drivers? If the (sub)woofer and mid-woofer can each put out 106 dB continuous and 109 dB peaks, they should be able to put out 109 dB continuous and 112 dB peaks together...?
Thanks in advance,
In my experience most decent PA drivers are limited to +20dB average gain and maybe another +6dB peak in their intended frequency range from a electrical perspective without burning up. The problem is usually either A) mechanical tolerance or B) distortion which I guess is much more difficult to anticipate. Most PA systems have subsonic filters to protect the bass. Hifi does not. Playing a 90dB 12” at 112dB without any protection it is doomed to get mechanical damage if the music have some peaks at 40Hz. I think if you want to have 112dB SPL and deep bass you need either a more sensitive bass driver and more power or a bigger driver, not for the sake of power handling but power usually also indicate mechanical tolerance and distortion. Never play more than 50% (have -3dB rms headroom).
Many companies also define peak as +6dB from RMS (4x power). It’s just a definition. In real life a peak is just something that adds dynamics to the perceived loudness which again is sensitive to human hearing, mostly the midrange. I would therefore find a more sensitive bass driver to match the mid because it’s actually the level of the distortion in the midrange which will eventually tell you to turn it down. You don’t want the bass to blow up while still have clear mids.
Regarding 2: +3dB will only happen where the drivers overlap in frequency if they are in phase. In other words if you have designed a good crossover it will not happen. One will take over where the other let go. The SPL are usually defined with a tolerance within a set frequency band for the intended use of the driver. Outside that band anything can happen (drops, peaks) and should be filtered out. If you have a 100dB 200Hz sine and a 100dB 2000Hz sine playing simultaneous it’s still just 100dB. The graphs are usually generated with a sine sweep. If you run pink noise instead that’s when the fun starts with artifacts harmonics and what not.
I think your calculation of the SPL for your woofer may need checking. 90 dB and 200 W continuous(ish) suggests more like 115 dB peak SPL at 1m rather than 106 dB. (If your get 90 dB with 1 W and a 3dB increase doubling power then a 256 W (peak) gives 114 dB. Adjust a bit for how sensitivity is defined and continuous(ish) to peak.)
If we want to limit ourselves to the published Xmax of 11 mm 0-pk, then this woofer is displacement limited to 107 dB at 32 Hz by my calculations. This is very close to your calculation of 106... close enough. At that point, the power demanded by the driver will be right at 200 W. However, above 40 Hz, the driver is capable of 111 dB with 200 W.
So the actual SPL capability of the driver will be program dependent (like any driver). Differing test standards will give different results. SB might have selected their "200 W" power limit based on the mechanical limits of the driver rather than the thermal limits. I suspect this might be true because the point where the driver exceeds Xmax happens to be about 200 W across a range of frequencies... plus this woofer has a 3 inch voice coil, and 200 W seems like a rather conservative thermal limit for a 3 inch voice coil.
In terms of dynamic capability, or headroom, we can operate a woofer beyond Xmax. The voice coil length is 28 mm, so half of that is 14mm. If the woofer is driven to +/- 14mm, the output would be 110 dB at 32 Hz, but you would need 300 W to get there.
So the actual SPL capability of the driver will be program dependent (like any driver). Differing test standards will give different results. SB might have selected their "200 W" power limit based on the mechanical limits of the driver rather than the thermal limits. I suspect this might be true because the point where the driver exceeds Xmax happens to be about 200 W across a range of frequencies... plus this woofer has a 3 inch voice coil, and 200 W seems like a rather conservative thermal limit for a 3 inch voice coil.
In terms of dynamic capability, or headroom, we can operate a woofer beyond Xmax. The voice coil length is 28 mm, so half of that is 14mm. If the woofer is driven to +/- 14mm, the output would be 110 dB at 32 Hz, but you would need 300 W to get there.
I am not trying to get the 12" driver to play at 112 dB (106 dB average, f3 @ 32 Hz is what I'm shooting for). I am trying to understand what manufacturers mean when they say that their product has 'x' dB peak SPL potential. Also in my simulation, I used an LR4 HPF at 20 Hz.
Take for example this 8" Genelec speaker which is specified as having a "Max Peak SPL" of 120 dB, which means this 8" woofer is putting out at least 114 dB @ 40 Hz... I guess it's not impossible, but it still makes me wonder how this "max peak spl" is calculated...
Another example (which I have brought up here before) is the JBL SCS8. If the "maximum SPL" rating is to be taken as is, this little speaker is putting out 115 dB @ 90 Hz...!
I think you might have inadvertently helped me get closer to what I'm looking to understand. Speaker SPLs are tested with pink noise and not sine waves, as far as I know. And pink noise has a crest factor of 6 dB, so the peaks should be 6 dB higher than the average SPL. So if a speaker can put out pink noise at 'x' dB SPL, it's "max peak SPL" should be x+6 dB SPL...
I'm almost certain I got something wrong here... waiting to be corrected.
This is how I calculated the SPL...
This is the SPL I got after LR4 HPF @ 20 Hz and + 2.5 dB @ 35 Hz.
According to the following simulation, at 67W power, Xmax has been reached. It got us an SPL of 106 dB with f3 @ ~32 Hz.
Have I got something wrong here?
Sorry if I misunderstood a few points in your original post (I tend to read only half the story due to my low attention span).
Id like to clarify.
106dB average @32Hz for a driver with 90dB sensitivity measured @100Hz will require quite a bit of power and power handling mostly mechanically using a sine wave but also electrically using pink noise. Especially if you bring in peaks as well (+6dB from a standard perspective, actual music program dynamics depends ALOT on genre, mastering trend from the decade etc). Thats why I said 112dB. You need that headroom to keep up with the pro mid. You also need more headroom to avoid distortion, but distortion at 32Hz is difficult for the human ear to detect, most likely you will hear harmonics and mechanical noises way before electrical clipping.
The examples you brought up with the JBL 8" coax driver is good. Its max peak at 114dB is +20dB from its sensitivity 94dB from 90Hz (100 watt). Assuming is has a subsonic filter. These peak measurement are using a known program such as sine sweep (mechanical testing) or continuous pink noise (electrical/thermal testing).
The Genelec example is tricky, its a powered monitor with adaptive subsonic filter/active compression/clipping as far as I know. They play flat until it plays nothing at all to protect the driver (at any given low frequency, its probably a 45Hz HPF as standard).
Some easy rules of thumbs that I use (sensitivity/SPL):
+3dB: 2x power (2^1)
+6dB: 4x power (2^2)
+9dB: 8x power (2^3)
+10dB: 10x power (10^1)
+20dB: 100x power (10^2)
+30dB: 1000x power (10^3) (or 4 times as "loud"!...)
Some more examples (power/RMS):
40 watt = 10+3+3 = +16dB (NAD, Rotel, Marantz integrated amps etc)
100 watt = 10+10 = +20dB (higher range HiFi amps)
128 watt = 3x7 = +21dB
200 watt = 10+10+3 = +23dB (smaller PA amps)
256 watt = 3x8 = +24dB
1000 watt = 10^3 = +30dB (3 BEL right*, definition of a BEL is doubling of percieved loudness I believe) (big PA amps, big guns)
Even if the industry have standardized on 6dB delta between peak and RMS for true music I think its better to allow at least 10dB headroom (double perceived dynamic range from average) in your system design so you can play music also from the good old days at loud levels without mechanically destroy the speaker. More modern music is compressed and require more from a thermal perspective than mechanically (clipping the peaks).
With this its all very easy.
For a 90dB driver to peak at 120dB it need to handle 1000 watt peak from a mechanical perspective with a sine sweep across the usable frequency range (I don't think any 12" will at 32Hz...).
For the same driver to average at at 110dB it needs to handle 100 watt RMS continuously with a pink noise program for electrical/thermal power handling for the same frequency range which usually is less of a problem.
The point is for a 12" to play 32Hz at all it needs to be a subwoofer design with a good xmax and power handling rather than sensitivity higher up around 100Hz.
Any system should be designed with atleast +20dB RMS and +30dB peak at any desired frequency response from max SPL target.
Then the sensitivity and size of speaker comes automatically.
In your case your sub fall to short in my opinion to keep up with the mid.
To me the mid decides the max SPL for the system as this is where the human ear is most sensitive to distortion, and the rest of the system should follow that.
I have no idea whether I got this all right but it usually helps me in PA and studio design to think this way.
Please someone correct me here, my theory is rusty old and based on a lot of pragmatic approach and experience rather than the books.
Id like to clarify.
106dB average @32Hz for a driver with 90dB sensitivity measured @100Hz will require quite a bit of power and power handling mostly mechanically using a sine wave but also electrically using pink noise. Especially if you bring in peaks as well (+6dB from a standard perspective, actual music program dynamics depends ALOT on genre, mastering trend from the decade etc). Thats why I said 112dB. You need that headroom to keep up with the pro mid. You also need more headroom to avoid distortion, but distortion at 32Hz is difficult for the human ear to detect, most likely you will hear harmonics and mechanical noises way before electrical clipping.
The examples you brought up with the JBL 8" coax driver is good. Its max peak at 114dB is +20dB from its sensitivity 94dB from 90Hz (100 watt). Assuming is has a subsonic filter. These peak measurement are using a known program such as sine sweep (mechanical testing) or continuous pink noise (electrical/thermal testing).
The Genelec example is tricky, its a powered monitor with adaptive subsonic filter/active compression/clipping as far as I know. They play flat until it plays nothing at all to protect the driver (at any given low frequency, its probably a 45Hz HPF as standard).
Some easy rules of thumbs that I use (sensitivity/SPL):
+3dB: 2x power (2^1)
+6dB: 4x power (2^2)
+9dB: 8x power (2^3)
+10dB: 10x power (10^1)
+20dB: 100x power (10^2)
+30dB: 1000x power (10^3) (or 4 times as "loud"!...)
Some more examples (power/RMS):
40 watt = 10+3+3 = +16dB (NAD, Rotel, Marantz integrated amps etc)
100 watt = 10+10 = +20dB (higher range HiFi amps)
128 watt = 3x7 = +21dB
200 watt = 10+10+3 = +23dB (smaller PA amps)
256 watt = 3x8 = +24dB
1000 watt = 10^3 = +30dB (3 BEL right*, definition of a BEL is doubling of percieved loudness I believe) (big PA amps, big guns)
Even if the industry have standardized on 6dB delta between peak and RMS for true music I think its better to allow at least 10dB headroom (double perceived dynamic range from average) in your system design so you can play music also from the good old days at loud levels without mechanically destroy the speaker. More modern music is compressed and require more from a thermal perspective than mechanically (clipping the peaks).
With this its all very easy.
For a 90dB driver to peak at 120dB it need to handle 1000 watt peak from a mechanical perspective with a sine sweep across the usable frequency range (I don't think any 12" will at 32Hz...).
For the same driver to average at at 110dB it needs to handle 100 watt RMS continuously with a pink noise program for electrical/thermal power handling for the same frequency range which usually is less of a problem.
The point is for a 12" to play 32Hz at all it needs to be a subwoofer design with a good xmax and power handling rather than sensitivity higher up around 100Hz.
Any system should be designed with atleast +20dB RMS and +30dB peak at any desired frequency response from max SPL target.
Then the sensitivity and size of speaker comes automatically.
In your case your sub fall to short in my opinion to keep up with the mid.
To me the mid decides the max SPL for the system as this is where the human ear is most sensitive to distortion, and the rest of the system should follow that.
I have no idea whether I got this all right but it usually helps me in PA and studio design to think this way.
Please someone correct me here, my theory is rusty old and based on a lot of pragmatic approach and experience rather than the books.
Last edited:
200 watt = 90+10+10+3 = 113dB peak but I think his point was -6dB peak gives 106 RMS.
I think this is the problem, mixing RMS and peaks. Industry standard claims for the most part (in pro) that peak is +6dB from RMS (in other words 4x power), however Hifi seems to use +3dB (2x power).
Most good music on the other hand have maybe +10dB headroom (10x power to deal with the peaks).
Yes 256w = +24dB (3dB x 8 "doublings").
Again I think the point is, find drivers which are as close as to each other in terms of:
- Sensitivity (in the intended spectrum)
- Power handling (in the intended spectrum)
- Mechanically suited for the job (in the intended spectrum, xmax etc).
= Max average and peak system SPL is an estimate based on the above.
Usually +20 (RMS) to +30 (peak) is what most are able to make with good compromises for sub especially.
This is why all PA systems have subsonic filters.
Because there is no useful content below 40Hz and hading systems to handle at decent levels it require a whole basement of 21" subwoofers. Which only elefants on the other content will detect anyway.
- Sensitivity (in the intended spectrum)
- Power handling (in the intended spectrum)
- Mechanically suited for the job (in the intended spectrum, xmax etc).
= Max average and peak system SPL is an estimate based on the above.
Usually +20 (RMS) to +30 (peak) is what most are able to make with good compromises for sub especially.
This is why all PA systems have subsonic filters.
Because there is no useful content below 40Hz and hading systems to handle at decent levels it require a whole basement of 21" subwoofers. Which only elefants on the other content will detect anyway.
Last edited:
Maybe this helps:
I think this is usually for HiFi.
For PA drivers its different.
Frequency response (IEC 268-5)
According to IEC 268-5, the frequency response of a loudspeaker is calculated as follows: 1) The frequency response of the loudspeaker is measured along the reference axis using a sine signal. 2) At the maximum sound pressure level, the volume level is averaged at one octave. This mean output level is termed the sensitivity. 3) The frequency response is given as the range of frequencies at which the volume level of the loudspeaker drops 10 dB below the sensitivity level. Dips in the frequency response narrower than 1/9 of an octave can be discounted.
For Faital:
Notes:
(1) 2 Hours Test According to AES 2-1984 Rev. 2003 (2) Maximum power is defined as 3dB greater than nominal power.
It means Faital have a different rating than Fane which use +6dB / 4x power for peak.
So peak rating is depending on the definition used by the vendor datasheet, not actual testing - only nominal rating is based on testing usually and rounding up to something that fit their marketing. Some not even that.
I think this is usually for HiFi.
For PA drivers its different.
Frequency response (IEC 268-5)
According to IEC 268-5, the frequency response of a loudspeaker is calculated as follows: 1) The frequency response of the loudspeaker is measured along the reference axis using a sine signal. 2) At the maximum sound pressure level, the volume level is averaged at one octave. This mean output level is termed the sensitivity. 3) The frequency response is given as the range of frequencies at which the volume level of the loudspeaker drops 10 dB below the sensitivity level. Dips in the frequency response narrower than 1/9 of an octave can be discounted.
For Faital:
Notes:
(1) 2 Hours Test According to AES 2-1984 Rev. 2003 (2) Maximum power is defined as 3dB greater than nominal power.
It means Faital have a different rating than Fane which use +6dB / 4x power for peak.
So peak rating is depending on the definition used by the vendor datasheet, not actual testing - only nominal rating is based on testing usually and rounding up to something that fit their marketing. Some not even that.
Last edited:
Example from a Fane driver:
Sensitivity (1W - 1m) Wideband 97.5 dB
Usable Frequency Range (-6dB) 45 Hz - 4.5 kHz
Power Handling 300 W (A.E.S.)
Program Power 600 W (A.E.S.)
Peak Power (6dB Crest Factor) 1200 W (A.E.S.)
But looking at the graph you see its actually 90dB at 60Hz.
Meaning you might get 300 watt RMS = 90+10+10+3+3 = 116dB and if your lucky 122 peaks if the xmax allows it.
This is a midbass not a sub. A sub will most likely have higher sensitivity in the <80Hz area but lower overall sensitivity and more power handling to compensate.
Sensitivity (1W - 1m) Wideband 97.5 dB
Usable Frequency Range (-6dB) 45 Hz - 4.5 kHz
Power Handling 300 W (A.E.S.)
Program Power 600 W (A.E.S.)
Peak Power (6dB Crest Factor) 1200 W (A.E.S.)
But looking at the graph you see its actually 90dB at 60Hz.
Meaning you might get 300 watt RMS = 90+10+10+3+3 = 116dB and if your lucky 122 peaks if the xmax allows it.
This is a midbass not a sub. A sub will most likely have higher sensitivity in the <80Hz area but lower overall sensitivity and more power handling to compensate.
Well we should start by assuming this SPL was measured with the most favorable program material or test signal. Since they do not specify what the signal was, we sould assume it is the best possible signal to generate the highest SPL. For example, pink noise with high pass filter at 80 Hz, or some such.
If they do not specify a distortion at that same SPL, we should assume the distortion could have been very high.
If they say "maximum SPL" without using the words "continuous", we should assume the max SPL was for a very short duration, like 2 seconds or less.
So what can we say about a speaker which is advertised at 115 dB peak SPL? If fed with the right kind of signal, it can produce 115 dB of noise at 1 meter for 1 second without beign destroyed. That is all I would assume. I would definately NOT assume that the speaker can produce musically relevant low distortion playback at 115 dB over its entire frequancy range for long periods of time.
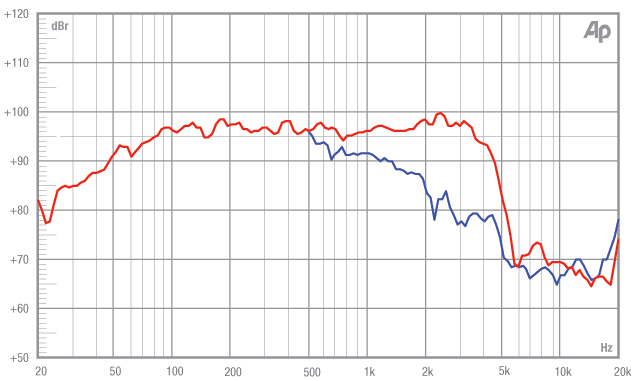
It may be a more a loss of plot rather than wrong. Perhaps the easiest way to get this across is to look at the actual performance of a well designed speaker similar to the one you are proposing. Consider the technical data for the KH 420.
The maximum SPL plot doesn't even bother to show the SPL at 30 Hz and yet you are assigning major significance to it to the extent you are not plotting the achievable SPL at higher frequencies (I think - it is your simulation). At this frequency the other main speaker, subwoofers, the room boundaries, etc... will all be contributing in the unlikely event there is any musical content down there. If there is it is likely to be fairly sustained with little requirement for a 20 dB or so peak:average margin.
Where you need large SPLs to handle transients is a bit higher in frequency where it exists in the music. Your 106 dB at 1 m will be insufficient for clean transients at standard levels listening at a few m away in a room. This is more a target for a desktop speaker. You should be looking for more like 115 dB at 1 m over the relevant frequencies which your driver can very likely deliver.
The KH 420 technical data quotes max. short term SPL with music material at 2.3 m in typical listening conditions (pair / full range) as 103 dB(C). This attempts to condense everything into a single number and is for a 10" driver where you have a 12". What is the estimated equivalent for your speaker?
I wrote a spreadsheet that overlaid the mechanical (excursion limited) and thermal (constant RMS) power handling of drivers in a 3 way. The idea was to overlay your acoustic response of each driver from your crossover and see where each touches the excursion/thermal limit lines of the spreadsheet (graph).
Whether the above is flawed or ideal... I don't know. Happy to share if you are interested.
Whether the above is flawed or ideal... I don't know. Happy to share if you are interested.
This is normally mid-band [~200 Hz typ. back in my day, so YMMV] and at least in this case it's for a pair [see description], so.......
10 log[540 W] = ~27.324 dB
120 dB - ~27.324 dB = ~92.676 dB - 3 dB paired sum = ~89.676 dB/W/M, ~111 dB/F6, which is quite reasonable for an 8".
PS Note the wide range of ways of expressing maximum SPL in the technical data varying from 90 dB to 122.4 dB depending on the details. The maximum SPL plot for 1%, 3% and 10% distortion is almost certainly the most useful but it is very rarely provided.
There is some discrepancy in our numbers. Though we have come to the same ~107 dB SPL figure for -3 dB @ 32 Hz, my calculator indicates that the power required for this is ~67W. This is with LR24 HPF @ 20 HZ and +2.5 dB @ 35 Hz.
Unfiltered 200W, when pushed into this speaker results in this excursion, with SPL hangnging at around 111 dB according to WinISD. Xmax has been reached @ ~45 Hz and XLim is at ~37 Hz. As it happens, Madisound's recommendation for a sealed box results in an f3 @ 37 Hz.
With a 200W signal, after applying LR24 HPF @ 21 Hz, The SPL is @ ~111 dB, but f3 is @ ~39 Hz... We're just about hitting Xlim.
Thoughts?
At least in theory since half of the sound power [1/f] is in the first [5] octaves and [for example] peak transient power of a large orchestra is in the 125 - 500 Hz BW with up to +30 dB [10x power] transients and even higher if a low B pipe organ is factored in, but aren't recordings just broadband limited to +5 - 25 dB dynamic headroom depending on a number of variables?
How To Build Speaker Enclosures By Alexix Badmaieff & Don Davis : Free Download, Borrow, and Streaming : Internet Archive
In short, with THX the dominant reference these days it seems reasonable to me to just figure based on its +30 dB for <120 Hz and +20 dB > 120 Hz unless one knows for sure that [much] less is required [radio, YouTube, certain types of music, etc.]