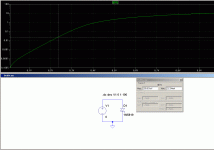
This is a simple question, but at this hour I can't figure out what I'm doing wrong.
I'm using LTspice to simulate a simple rectifier circuit using a sine wave generator (24 V, 50 Hz), a full wave diode bridge, a reservoir capacitor (2200 µF) and a load resistor (1k).
I was expecting to see approximately 24 * sqrt(2) - 2 * 0.65 (diode drop) = 32.5 V, across the load resistor (plus some ripple).
Instead, I'm seeing 23.3 V.
What am I doing/thinking wrong?
Screenshot attached.
Regards,
Alexander
I'm using LTspice to simulate a simple rectifier circuit using a sine wave generator (24 V, 50 Hz), a full wave diode bridge, a reservoir capacitor (2200 µF) and a load resistor (1k).
I was expecting to see approximately 24 * sqrt(2) - 2 * 0.65 (diode drop) = 32.5 V, across the load resistor (plus some ripple).
Instead, I'm seeing 23.3 V.
What am I doing/thinking wrong?
Screenshot attached.
Regards,
Alexander
Attachments
24 V is the amplitude of the sine source - ie the peak values are +/-24 V
you have to multiply your argument in the sine source parameter list by sqrt(2) if you want "rms"
you have to multiply your argument in the sine source parameter list by sqrt(2) if you want "rms"
Yoiu should enter the PEAK value for the sine's AMPLITUDE field, in the AC voltage source, not the RMS value.
Yes. The entered value shows 24V which is the peak value. For 24VRMS he should enter about 34V peak (or 24V RMS; not sure you can spec RMS in LTspice).
jd
Well, of course. Thank you! 🙂
Ever since I started playing/working with electronics (which isn't many years, but still), I've had the intuitive view of the RMS voltage of an AC signal, as a rectangle which occupies the same area under the graph as a sine wave does over the same range.
Mathematically speaking; integrate abs(sin(x)) (a rectified sine wave) over the range of 0 to a (a = 2*pi*k), and divide the sum by a to get the height/amplitude of the rectangle that you've created.
Example:
Integrate abs(sin(x)) over 0 to 2*pi = 4.
Divide 4 by 2*pi = 2/pi ≈ 0.637.
0.637 V would then be the RMS voltage of an AC signal with a peak voltage of 1 V.
I did some calculations and found this terribly wrong.
The real RMS voltage of an AC signal with a Vpk of 1 V is 1/sqrt(2) ≈ 0.707 V.
What am I missing?
Ever since I started playing/working with electronics (which isn't many years, but still), I've had the intuitive view of the RMS voltage of an AC signal, as a rectangle which occupies the same area under the graph as a sine wave does over the same range.
Mathematically speaking; integrate abs(sin(x)) (a rectified sine wave) over the range of 0 to a (a = 2*pi*k), and divide the sum by a to get the height/amplitude of the rectangle that you've created.
Example:
Integrate abs(sin(x)) over 0 to 2*pi = 4.
Divide 4 by 2*pi = 2/pi ≈ 0.637.
0.637 V would then be the RMS voltage of an AC signal with a peak voltage of 1 V.
I did some calculations and found this terribly wrong.
The real RMS voltage of an AC signal with a Vpk of 1 V is 1/sqrt(2) ≈ 0.707 V.
What am I missing?
Probably because those are Schottky diodes, and because the current is quite low. Forward voltage drop is a function of the forward current.
I'm sure Spice aficionados can chime in here, but I'd prefer to say that "the model used for the diodes result in a 350mV drop at 23.3mA". LTSpice isn't really reporting the voltage drop across the diodes. It uses whatever the model tells it to.
RMS = Root Mean Square, in other words, it is the square root of the average (mean) of the Square of the signal.
Why square the sine instead of just taking the average of the absolute value? Because power is proportional V squared, not proportional to V. That's why 1 Volt AC RMS delivers the same power into a load as 1 Volt DC.
Your intuitive view is just slightly off. If you apply the same logic to the square of the sine wave (and of square wave) I think that you will get the result you expected.
Why square the sine instead of just taking the average of the absolute value? Because power is proportional V squared, not proportional to V. That's why 1 Volt AC RMS delivers the same power into a load as 1 Volt DC.
Your intuitive view is just slightly off. If you apply the same logic to the square of the sine wave (and of square wave) I think that you will get the result you expected.
Thank you for refreshing my memory macboy!
To reduce rounding error (by typing in an approximation to 24*sqrt(2)) I replaced the AC voltage source with an "Arbitrary behavioral voltage source".
BV1 N00x N00y V=24*sqrt(2)*sin(2*pi*50*time)
AndrewT:
Unloaded (except for the capacitor) the diodes drops 146.7 mV each. Loaded by a 1 A active load they drop 1.53 V each.
I did, right on the spot. 🙂
To reduce rounding error (by typing in an approximation to 24*sqrt(2)) I replaced the AC voltage source with an "Arbitrary behavioral voltage source".
BV1 N00x N00y V=24*sqrt(2)*sin(2*pi*50*time)
AndrewT:
Unloaded (except for the capacitor) the diodes drops 146.7 mV each. Loaded by a 1 A active load they drop 1.53 V each.
<Grin!> If you're worrying about arbitrarily-small rounding errors like that (you could just enter a few more digits, instead, you know), maybe you should also set the maximum timestep to something smaller than the default, if you haven't already. Maybe try something like .01 to .001 times the shortest period involved, so .0001 or .00001 second.
And if you think that you can really get so many significant digits from the simulator, then you really should also model all of the non-ideal and parasitic characteristics of everything, such as the distributed inductance and resistance of the conductors, the equivalent parallel capacitances of any resistors, the equivalent series resistance and parallel inductance of each capacitor, an actual AC mains transformer, and so on and so on. Of course, the capcitors' ESRs will vary with frequency and temperature, so you'd need to model that, too, in general.
I was just joking around. But, actually, that can all be done, even in LTspice. But it gets "messy" quite quickly. And the simulation runs will slow to a relative crawl, especially if higher frequencies are involved.
Here's a fun thing to do: Test your power supply by adding a load that consists of a pulse or square wave current source with fast edge times, drawing current from the supply through a small resistance (maybe 8 ohms?). Then maybe try adding a few of the parasitic components, such as the conductors' inductances (maybe 25 nH per inch).
P.S. There are a lot of _very_ interesting and extremely useful old message threads, and a lot of interesting and useful files, in the archives of the LT_Spice discussion group. I have a link to that, and to two places with tens of thousands of downloadable spice models, at Spice Component and Circuit Modeling and Simulation .
(Please note that regardless of what might appear on my other pages that are linked from there, I am no longer selling anything at all from any of my web pages.)
Cheers,
Tom
And if you think that you can really get so many significant digits from the simulator, then you really should also model all of the non-ideal and parasitic characteristics of everything, such as the distributed inductance and resistance of the conductors, the equivalent parallel capacitances of any resistors, the equivalent series resistance and parallel inductance of each capacitor, an actual AC mains transformer, and so on and so on. Of course, the capcitors' ESRs will vary with frequency and temperature, so you'd need to model that, too, in general.
I was just joking around. But, actually, that can all be done, even in LTspice. But it gets "messy" quite quickly. And the simulation runs will slow to a relative crawl, especially if higher frequencies are involved.
Here's a fun thing to do: Test your power supply by adding a load that consists of a pulse or square wave current source with fast edge times, drawing current from the supply through a small resistance (maybe 8 ohms?). Then maybe try adding a few of the parasitic components, such as the conductors' inductances (maybe 25 nH per inch).
P.S. There are a lot of _very_ interesting and extremely useful old message threads, and a lot of interesting and useful files, in the archives of the LT_Spice discussion group. I have a link to that, and to two places with tens of thousands of downloadable spice models, at Spice Component and Circuit Modeling and Simulation .
(Please note that regardless of what might appear on my other pages that are linked from there, I am no longer selling anything at all from any of my web pages.)
Cheers,
Tom
Last edited:
You can easily plot the characteristic of any component in the library:
Attachments
- Status
- Not open for further replies.