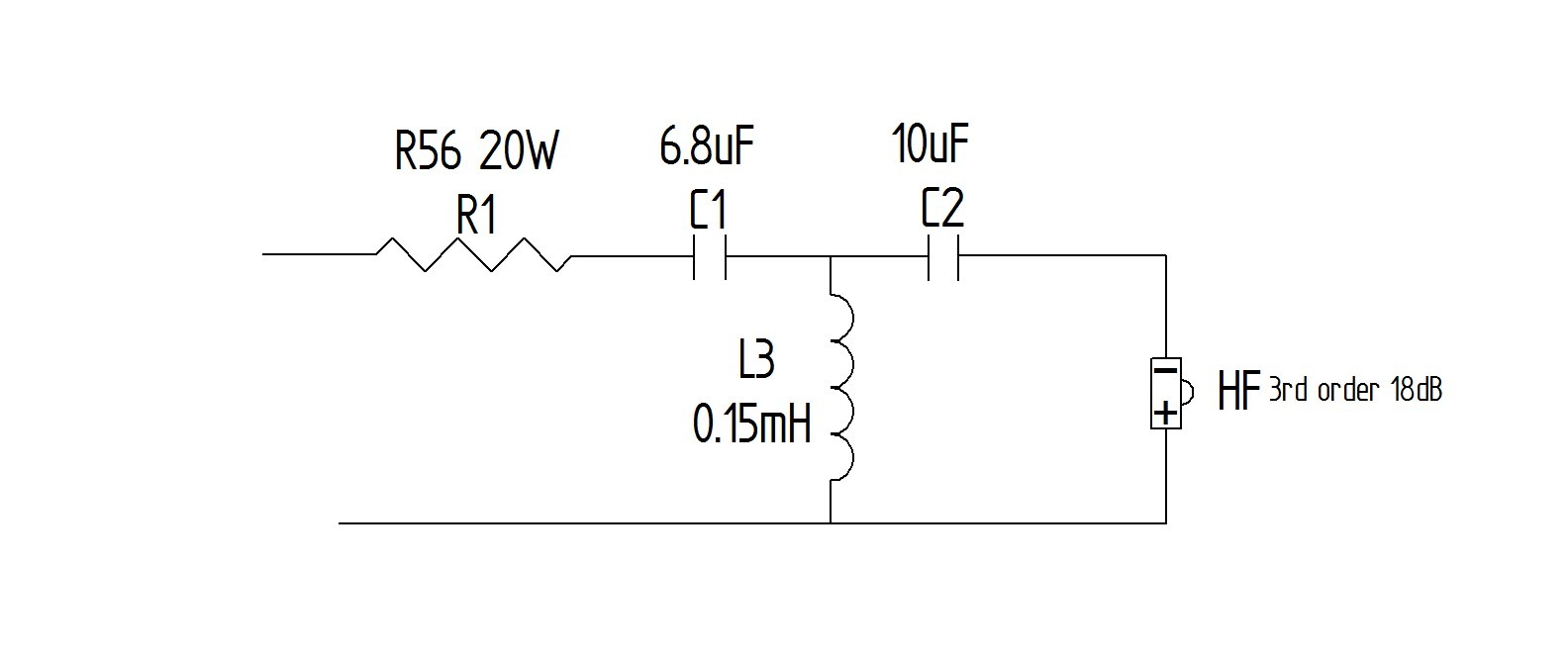
Hi all. do I know what I'm doing? So I looked at schematics of Linkwitz-Riley 3rd order and butterworth 3rd order crossovers for tweeters and they appear to be the same. Is the only difference the values of the caps and inductors? Attached is the schematic of my outboard XO which looks like the schematics for LR and Butterworth I've seen. Then again I may be totally wrong and not understanding the schematics.
Last edited:
Audio control.com has a white paper on it. Butterworth is maximally flat amplitude ie no ripple in pass band and a controlled roll off. It has phase and delay issues. Bessel has maximally flat phase. LR has great impulse response. It goes on and on so check out https://www.audiocontrol.com/downloads/tech-papers/tech-paper-102.pdf
Thanks for the info but they both look the same so is the difference in the values of the caps and inductors?
Last edited:
Sticking to the example you asked about, there is technically no such thing as a 3rd order Linkwitz filter, as he & Riley only worked with even order types, which is why they're sometimes called squared Butterworth filters. However, you can create a quasi-3rd order Linkwitz. 3rd order Butterworth has the phase at either 90 or 270 degrees, and sums flat at -3dB. A quasi 3rd order Linkwitz will have a complimentary phase response, and the filters down -6dB at the crossover frequency. It can work quite well in practice.
Yes, the reactance of the parts makes the difference. One component per order. Third order means three components.
Agreed no real LR3. Quasi can be done.
LR sums flat with -6dB summation, generally 0.5 Q, phase aligned in quadrature.
BW sums vary with order, 0.707 Q, phase alignment 90° out.
LR sums flat with -6dB summation, generally 0.5 Q, phase aligned in quadrature.
BW sums vary with order, 0.707 Q, phase alignment 90° out.
Yes for even order filters. For odd order, another difference is that odd-order Linkwitz-Riley filters don't exist while Butterworth filters do exist.
So I would like to try a Linkwitz Riley 3-way 2nd order XO but after trying various calculators i got varying results with varying schematics. Some had many components and some had fewer components. What would a parallel LR2 XO look like for a 3-way speaker with crossovers at 150 hz and 300hz for 8 ohm drivers?
thanks,
Henry
thanks,
Henry
Thanks for the info but what does a 3-way XO look like. That is what does the pass band look like?
150 and 300 Hz ?
That doesn't make much sense for a 3 way.
Linkwitz Riley just has a filter Q of .5
Far as the very generic filter topology of a 2nd order 3 way
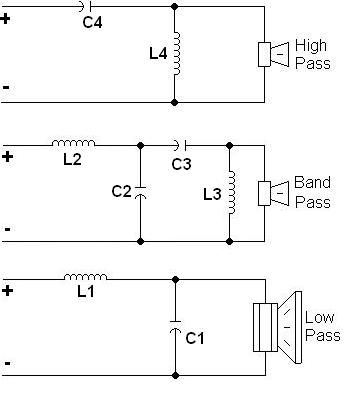
To answer your first question, yes the topology of the filter is the same.
And yes the inductor and capacitor values would slightly change.
To change the Q of the filter cutoff.
Linkwitz Riley Filter has a Q of .5
Butterworth Filter has a Q of .707
Additional components could include padding resistors to match driver levels
Impedance compensation, Baffle compensation, notch filters etc etc.
Every driver is different.
Generic filter calculators usually don't yield optimal results
Might be more useful to describe your project
and what drivers your using.
That doesn't make much sense for a 3 way.
Linkwitz Riley just has a filter Q of .5
Far as the very generic filter topology of a 2nd order 3 way
To answer your first question, yes the topology of the filter is the same.
And yes the inductor and capacitor values would slightly change.
To change the Q of the filter cutoff.
Linkwitz Riley Filter has a Q of .5
Butterworth Filter has a Q of .707
Additional components could include padding resistors to match driver levels
Impedance compensation, Baffle compensation, notch filters etc etc.
Every driver is different.
Generic filter calculators usually don't yield optimal results
Might be more useful to describe your project
and what drivers your using.
Last edited:
Don’t forget the difference in power response. Which is a flaw in LR setups. Butterworth does notably better.
Ideally, Butterworth crossover filters keep the sum of the powers from the drivers constant. That causes a peak in the on-axis response with even-order filters and depending on the driver placement, a rotated main lobe with odd-order filters.
By design, Linkwitz-Riley filters keep the magnitude of the sum of the sound pressures on axis constant, ideally anyway, but cause a dip in the sum of the powers.
By design, Linkwitz-Riley filters keep the magnitude of the sum of the sound pressures on axis constant, ideally anyway, but cause a dip in the sum of the powers.
Probably not generally known, but since we understand the importance of the power response (thx Toole e.a.) this has become quite relevant in speaker design.
