I've often wondered if there is a way to model the cavity resonance that tends to affect the response of folded open baffle woofers, such as H-frames, and perhaps U-frames and even ripoles. I've looked for info on diyaudio from time to time, but until recently had never picked up anything very useful. I have tried Hornresp, but found it limited to a few specific geometries. (Maybe that's just a reflection of my small experience with it.)
My (poor) knowledge of open baffle theory has mostly come from reading Linkwitz Lab, and I have a vague memory of Siegfried suggesting that it's the length (front to back) of a cavity that is the primary determinant of cavity resonances. But I was pretty sure I'd also read a comment from him to the effect that measured results didn't match theory very well. (Which doesn't bode well for modelling.)
Anyway, I went back to the Linkwitz Lab site and, sure enough, found this page: https://www.linkwitzlab.com/models.htm#C
Siegfried said, there: "If you build an H baffle woofer ... there will also be a response peak due to a l/4 resonance of the waveguides in front and behind the drivers."
He then shows a nearfield response measurement of his Phoenix woofer baffle (a W-frame, actually) showing just such a peak:
He comments: "The PHOENIX woofer has D=19" (0.48 m) separation between its openings. The peak should be at f = 0.5*v/D = 357 Hz, but the cabinet layout is too complicated for such simple calculation to apply exactly."
This is what I read years ago. Going back to it, though, had me really scratching my head. The peak is nowhere near 357Hz, but also, I don't actually understand why SL said initially it's a l/4 resonance, (which is what you'd expect for a pipe open at one end) but then calculated the expected frequency as l/2.
So I was no further forward.
Recently, however, I stumbled across an old thread here on diyaudio which addresses the very question of cavity resonance:
https://www.diyaudio.com/community/threads/ripole-cavity-resonance-question.240193/
This got my hopes up. I was particularly pleased when saw that an answer to the question of how to calculate cavity resonance was offered by @bolserst. This is a key part of what he had to say:
"The cavity resonance is ... a Helmholtz type resonance which develops because the air inside the cavity acts like a spring and the air at the opening of the cavity acts like a mass. You can think of it as a vented or ported box with port length zero and port area the size of the opening. With this in mind, you can get an estimate of what the cavity resonance would be by using a calculator for a vented box. Just set the volume of the box equal to the volume of the cavity, and the area of the port equal to the area of the cavity opening. Then solve for the tuning frequency that gets you a port length of zero."
He also comments that quarter-wave theory only begins to apply when the cavity geometry is more pipe-like. It struck me immediately that this is a much more promising way of thinking about cavity resonances.
The next thing I realised was that there is an easy way for me to model them, because I'm familiar with how to model vented boxes in Basta! So, I fired up Basta! and had a go, and the results are very encouraging. The method I've settled on is actually not to model a cavity as a simple vented box. (Although you can if you like. However you'll get a rather 'busy' graph from that, with driver and vent responses, and a combined response that rolls off the low frequencies, but doesn't reflect the baffle dimensions.) A better way is actually to model a bandpass box with a single vent, and with the volume of the rear enclosure set very large. Like this:
In this model, the driver behaviour is not constrained by the rear box volume, because Vb2 is set so large. The response curve you get is the response of the vent. You set Vb to your best estimate of the volume of the cavity, and then in the Vent/PR tab, you set the vent cross-sectional area to match the area you calculate for the cavity mouth. Then adjust the vent tuning frequency until the vent length is approximately zero.
I did this for the Phoenix woofer box (with a fair bit of guess-work) and got the response shown above. As you can see, it's not a bad match for Siegried's measured response. (There is actually a slight broadening of the resonance, because the Phoenix W-baffle dimensions generate slightly different resonances front and back. Siegfied's measurements show even more of a broadening in the resonance than my model did.) Note that the modelled response does not take account of the rear driver radiation, and therefore doesn't show the dipole roll-off at low frequencies. But Siegfried's measured response was near-field, so it doesn't show the dipole roll-off either. (You can model the dipole roll-off in Basta! by selecting "Baffle" as the enclosure type. You just can't model the roll-off and the cavity resonance at the same time.)
So, anyway, I'm extremely grateful to bolserst for getting me thinking more clearly about cavity resonances. And I can recommend Basta! as a simple way to generate a rough model. I'm hopeful it's reasonably accurate. When I get some time I'll do a few measurements of my own and see how well they match the modelling.
My (poor) knowledge of open baffle theory has mostly come from reading Linkwitz Lab, and I have a vague memory of Siegfried suggesting that it's the length (front to back) of a cavity that is the primary determinant of cavity resonances. But I was pretty sure I'd also read a comment from him to the effect that measured results didn't match theory very well. (Which doesn't bode well for modelling.)
Anyway, I went back to the Linkwitz Lab site and, sure enough, found this page: https://www.linkwitzlab.com/models.htm#C
Siegfried said, there: "If you build an H baffle woofer ... there will also be a response peak due to a l/4 resonance of the waveguides in front and behind the drivers."
He then shows a nearfield response measurement of his Phoenix woofer baffle (a W-frame, actually) showing just such a peak:
He comments: "The PHOENIX woofer has D=19" (0.48 m) separation between its openings. The peak should be at f = 0.5*v/D = 357 Hz, but the cabinet layout is too complicated for such simple calculation to apply exactly."
This is what I read years ago. Going back to it, though, had me really scratching my head. The peak is nowhere near 357Hz, but also, I don't actually understand why SL said initially it's a l/4 resonance, (which is what you'd expect for a pipe open at one end) but then calculated the expected frequency as l/2.
So I was no further forward.
Recently, however, I stumbled across an old thread here on diyaudio which addresses the very question of cavity resonance:
https://www.diyaudio.com/community/threads/ripole-cavity-resonance-question.240193/
This got my hopes up. I was particularly pleased when saw that an answer to the question of how to calculate cavity resonance was offered by @bolserst. This is a key part of what he had to say:
"The cavity resonance is ... a Helmholtz type resonance which develops because the air inside the cavity acts like a spring and the air at the opening of the cavity acts like a mass. You can think of it as a vented or ported box with port length zero and port area the size of the opening. With this in mind, you can get an estimate of what the cavity resonance would be by using a calculator for a vented box. Just set the volume of the box equal to the volume of the cavity, and the area of the port equal to the area of the cavity opening. Then solve for the tuning frequency that gets you a port length of zero."
He also comments that quarter-wave theory only begins to apply when the cavity geometry is more pipe-like. It struck me immediately that this is a much more promising way of thinking about cavity resonances.
The next thing I realised was that there is an easy way for me to model them, because I'm familiar with how to model vented boxes in Basta! So, I fired up Basta! and had a go, and the results are very encouraging. The method I've settled on is actually not to model a cavity as a simple vented box. (Although you can if you like. However you'll get a rather 'busy' graph from that, with driver and vent responses, and a combined response that rolls off the low frequencies, but doesn't reflect the baffle dimensions.) A better way is actually to model a bandpass box with a single vent, and with the volume of the rear enclosure set very large. Like this:
In this model, the driver behaviour is not constrained by the rear box volume, because Vb2 is set so large. The response curve you get is the response of the vent. You set Vb to your best estimate of the volume of the cavity, and then in the Vent/PR tab, you set the vent cross-sectional area to match the area you calculate for the cavity mouth. Then adjust the vent tuning frequency until the vent length is approximately zero.
I did this for the Phoenix woofer box (with a fair bit of guess-work) and got the response shown above. As you can see, it's not a bad match for Siegried's measured response. (There is actually a slight broadening of the resonance, because the Phoenix W-baffle dimensions generate slightly different resonances front and back. Siegfied's measurements show even more of a broadening in the resonance than my model did.) Note that the modelled response does not take account of the rear driver radiation, and therefore doesn't show the dipole roll-off at low frequencies. But Siegfried's measured response was near-field, so it doesn't show the dipole roll-off either. (You can model the dipole roll-off in Basta! by selecting "Baffle" as the enclosure type. You just can't model the roll-off and the cavity resonance at the same time.)
So, anyway, I'm extremely grateful to bolserst for getting me thinking more clearly about cavity resonances. And I can recommend Basta! as a simple way to generate a rough model. I'm hopeful it's reasonably accurate. When I get some time I'll do a few measurements of my own and see how well they match the modelling.
Attachments
Last edited:
Hornresp can simulate H-Frame, U-Frame and Ripole loudspeakers taking enclosure "cavity" resonances into account.
Thanks David, yes, I've has a go at that. I couldn't see a way to play around with the geometry, though. For example the Linkwitz Phoenix has different cavities front and back. And I wanted to try modelling the likes of the XSD speaker which has small cavities at the front, and bigger ones created by wings at the back, or Perry Marshall's Bitches Brew, which is a U baffle of sorts, with slanted wings.
Siegfried Linkwitz put some of his analysis of H and U frame woofers here: https://www.linkwitzlab.com/frontiers.htm#L and here: https://www.linkwitzlab.com/H-U woofer2.htm His analysis is impressive, as his work so often was.
But if @bolserst is correct, and folded baffle cavity resonances can be modelled as Helmholz type resonances, SL appears to have missed that. No?
Of course, Basta! is just one of many programs/utilities that can model vented boxes - I happen to like it a lot for its ease of use. I'm going to play more with Hornresp, perhaps using the MLTL wizard, because (if I've got this right) it will model both pipe and Helmzolz behaviour.
But if @bolserst is correct, and folded baffle cavity resonances can be modelled as Helmholz type resonances, SL appears to have missed that. No?
Of course, Basta! is just one of many programs/utilities that can model vented boxes - I happen to like it a lot for its ease of use. I'm going to play more with Hornresp, perhaps using the MLTL wizard, because (if I've got this right) it will model both pipe and Helmzolz behaviour.
OK, here's a quick attempt in Hornresp, using the input wizard, and modelling the front output of the Phoenix woofer unit as if it were an MLTL. The screenshot has both Basta and Hornresp models showing. In Hornresp, I'm showing Input 1, which is the front radiation.
(Note: if you compare the Hornresp prediction to SL's actual near-field measurement of the front output, in post #1 above, there's a remarkably good correlation above the main resonant peak - see the null around 500 Hz and the peaks above that. This is impressive!)
But if I show the Combined response, and use the Path Length feature to adjust for the effective baffle size, I should get a decent prediction of both the cavity behaviour and the dipole roll-off. Here you go:
Edit: I just realised I only entered one driver when doing the Hornresp model instead of a pair. That'll have thrown things off a little. Still, it looks like the method works pretty well.
(Note: if you compare the Hornresp prediction to SL's actual near-field measurement of the front output, in post #1 above, there's a remarkably good correlation above the main resonant peak - see the null around 500 Hz and the peaks above that. This is impressive!)
But if I show the Combined response, and use the Path Length feature to adjust for the effective baffle size, I should get a decent prediction of both the cavity behaviour and the dipole roll-off. Here you go:
Edit: I just realised I only entered one driver when doing the Hornresp model instead of a pair. That'll have thrown things off a little. Still, it looks like the method works pretty well.
Last edited:
You are most welcome.
Looks like you are on the right track now with either Basta! or Hornresp.
One additional comment I will add is that the effective mass at the opening of the cavity(ie the reactive part of the radiation impedance) is dependent on the radiation space the H-Baffle is radiating into. Hornresp allows you to set this so you can better model the cavity resonance. I'm not sure if Basta! has this ability, but I couldn't locate mention of it in the online user's guide.
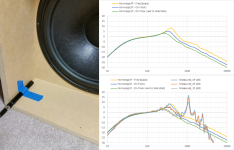
Here is an example showing measurements for cavity resonance of H-frame measured 3 ways, vs the Hornresp predictions.
You can see that as the radiation space gets smaller the radiation impedance increases. This increases the effective mass and damping (ie lowers frequency and magnitude of cavity resonance)
Note that the response peak just above 1kHz is the first SLS12 cone break-up mode, so not anything to do with the cavity resonance.
More details on modeling of H-baffle with Hornresp here: https://www.diyaudio.com/community/threads/hornresp.119854/post-5923396
You may also find the U-frame modeling capability of interest: https://www.diyaudio.com/community/threads/hornresp.119854/post-6166811
Just for the record, the H-Frame and U-Frame models used in Hornresp were developed, and very kindly provided to me, by bolserst.
Is that the microphone (the black tube held down with blue tape) in the picture? If so, that is the wrong place to make the measurement if the pickup is near the baffle that the woofer is mounted to. The mic pickup should be located in the plane of the opening of the H-frame, or even a couple of inches farther out into the room (because there is an "end effect" just like with a port).
I corrected the Hornresp model so it has a pair of drivers (in parallel) rather than a single driver. Here's the plot:
Output is up, impedance down - as you'd expect - but also the centre frequency of the resonance has moved up from about 208 Hz to 226 Hz, (which is much closer to the Basta! prediction).
Output is up, impedance down - as you'd expect - but also the centre frequency of the resonance has moved up from about 208 Hz to 226 Hz, (which is much closer to the Basta! prediction).
Good eye! Yes, that is a LinearX M51 microphone that I often use for measuring inside of cavities and ports due to its small size. As long as frequency of interest has wavelength > 10x the length of the frame or port( or distance from port exit), the measured response is essentially identical. At high frequencies the measured pressure response will diverge. For an extreme example see post concerning response at the input and output of a 1.6m long port.
https://www.diyaudio.com/community/...tween-winisd-hornresponse.311268/post-5169553
The mic in the picture was being used to improve measurement fidelity at low frequencies by splicing together measurements near the cavity pressure boundary and in exit plane of cavity to remove as much as possible the contamination of the acoustic output of the other side of the dipole woofer. Even so, you can still notice the LF roll-off slope not quite matching the expected -12dB/oct roll-off.
No doubt you have attempted to measure response of front baffle mounted ports that get contaminated by the nearby woofer output. You can measure inside the port to improve the situation, but do need to be aware of the 10x rule for the upper frequency limit of valid data.