I am searching for PC based tone generator that will allow adding multiple tones with variable amplitude. For example, 1Khz at -3db, 2Khz at -40db, etc...
Also it has to be capable of creating tones at 92Khz or higher also.
Right now I have the NCH Tone Generator that has multiple tones and variable amplitude but unfortunately its fixed at 44.1Khz so can't add any frequency above Fs/2.
Any help greatly appreciated!
TiA!
Also it has to be capable of creating tones at 92Khz or higher also.
Right now I have the NCH Tone Generator that has multiple tones and variable amplitude but unfortunately its fixed at 44.1Khz so can't add any frequency above Fs/2.
Any help greatly appreciated!
TiA!
if you intend to use a sound card fs/2 will be just one limit, even 192K cards may not put out much at 92KHz because of digital filters internal to the ADC chips often set at 0.4*fs
LtSpice, SciLab are 2 freeware options that can create .wav files
Audacity can play/record - although I've seen dropouts at 192KHz
LtSpice, SciLab are 2 freeware options that can create .wav files
Audacity can play/record - although I've seen dropouts at 192KHz
brain fart...when I wrote 92khz I wanted to write 96khz but was thinking 192khz.
for now anything that behaves well at 96khz should serve the purpose.
for now anything that behaves well at 96khz should serve the purpose.
actually I should have written ADCs and DACs - on soundcards both are typically oversampling internally and have digital filtering below fs/2 built in
you will have 0 output in any sampled system at fs/2 = 96 KHz with a 192K soundcard
you will have 0 output in any sampled system at fs/2 = 96 KHz with a 192K soundcard
well I could get ETG (expression tone generator) and GoldWave to generate complex tones at a 96Khz sample rate. Basically they both have expression evaluators so lots of flexibility on the type of signal you want to create. But there's one problem -
I see distortion when I do a spectrum analysis of the resulting wav file. (fft of the just the static wav file, not by playing/recording the signal). I was expecting that when I generate a 1Khz sine tone, all I would see in the fft is one fundamental at 1Khz and nothing else but instead I see harmonics at 3khz, 5khz,.. I noticed this happens is in both GW and ETG.
What could cause this ? My only guess is insufficient precision in the sinusoidal function used to compute the sample values ?? Is that possible ?
p.s.:- I haven't tried Ltspice or Scilab, but do you think they have what I want ?
I see distortion when I do a spectrum analysis of the resulting wav file. (fft of the just the static wav file, not by playing/recording the signal). I was expecting that when I generate a 1Khz sine tone, all I would see in the fft is one fundamental at 1Khz and nothing else but instead I see harmonics at 3khz, 5khz,.. I noticed this happens is in both GW and ETG.
What could cause this ? My only guess is insufficient precision in the sinusoidal function used to compute the sample values ?? Is that possible ?
p.s.:- I haven't tried Ltspice or Scilab, but do you think they have what I want ?
I'd expect most packages to work equally well within some limits: the quantization will give some distortion content ~ 1 bit amplitude level - and windowing issues with the fft can give apparent "spurs" from spectral spreading if you don't use exact integer fundamental cycles in your ftt
it's possible that biased rounding or other math error could contribute too but for 16 bit resolution, 32 bit math should be OK
at 24 bits the math may need to be 64 bit
it's possible that biased rounding or other math error could contribute too but for 16 bit resolution, 32 bit math should be OK
at 24 bits the math may need to be 64 bit
It appears some people can mess up truncation/rounding - LtSpice has a problem with 16 bit wav files, not 8 or 24!
Mike's usually fast with fixes - I hope this is cleared up by the next release (sometimes weekly)
I guess other tools could have similar problems - always verify, correct numerical implementations really follow the theory to a fine degree
Mike's usually fast with fixes - I hope this is cleared up by the next release (sometimes weekly)
I guess other tools could have similar problems - always verify, correct numerical implementations really follow the theory to a fine degree
Hi,
If I'm right to think that all digital signals start as square waves added together to form an approximation of a sinewave then there must always be measurable distortion of the filtered output signal.
The higher the sinewave frequency, the fewer squarewaves to approximate the wave shape, the worse the distortion.
The lower the level, the fewer steps available for each increment of voltage and again the worse the distortion.
It seems that all HF signals generated digitally must by design have significant distortion that worsens as the Fs/2 limit is approached.
I cannot see how 192kHz square waves can ever produce a 96kHz sinewave even with a high slope analogue filter hung on the end of the DAC.
If I'm right to think that all digital signals start as square waves added together to form an approximation of a sinewave then there must always be measurable distortion of the filtered output signal.
The higher the sinewave frequency, the fewer squarewaves to approximate the wave shape, the worse the distortion.
The lower the level, the fewer steps available for each increment of voltage and again the worse the distortion.
It seems that all HF signals generated digitally must by design have significant distortion that worsens as the Fs/2 limit is approached.
I cannot see how 192kHz square waves can ever produce a 96kHz sinewave even with a high slope analogue filter hung on the end of the DAC.
still haven't tried LTspice or Scilab but ended up writing a script to generate my own sine wave! I even wrote my own function to calculate sine based on taylor series. Its interesting how much precision (atleast 7 digits after the decimal point for 16 bit depth) is required to avoid rounding errors and take the precision upto or less than 1LSB.
I have yet to add the file creation part to write to a pcm wav file. Once that is done I will know how much distortion there is in the produced wave, or lack thereoff.
In v2.0, complex waves - ability to add harmonics with variable amplitude!
I wonder if these packages, or the languages they are written in, have the kind of precision for these type of operations.
I have yet to add the file creation part to write to a pcm wav file. Once that is done I will know how much distortion there is in the produced wave, or lack thereoff.
In v2.0, complex waves - ability to add harmonics with variable amplitude!
I wonder if these packages, or the languages they are written in, have the kind of precision for these type of operations.
not when the system (DAC) is trying to reconstruct an analogue signal (sinewave) from a digital datastream.Pan said:
If you do breakdown a squarewave into it's components one finds that the harmonics go out to infinity. That is the problem. The digital datastream runs out of bits in the range of 44Ks/S to 192ks/S. I have seen it estimated that a good approximation to a squarewave can be reconstructed if all the harmonics up to the tenth are included in the signal. To reconstruct a reasonable 96kHz squarewave would require a bit rate of 1Ms/S or looked at from CD datarates it should be possible to get a 4kHz squarewave from the DAC. I suspect that even a 4kHz sinewave coming out of a CD DAC will show significant distortion.
Does anyone have any figures?
6 digits of precision(i.e. after the decimal point) and processing the sine series(taylor polynomial) up to the 9th degree is what you need in the least to create a sine wave with distortion buried in the noise floor.
Note that I did not say "without distortion". It is there, just not discernable.
I had been fooling around with creating a wav file of a pure tone and observing what kind of loss of precision generates what kind of distortion and thought I'd share some results with you.
It is a common belief that computing upto the 7th degree of the Taylor series for a sine function is a good enough approximation for a sine function.
Wrong. You need alteast one more degree i.e. upto 9th degree to achieve a sine wave which has very little distortion.
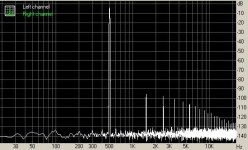
Here's a screen shot of the FFT of a 500hz sine wave produced with the sine function computing only upto the 7th degree -
Note that I did not say "without distortion". It is there, just not discernable.
I had been fooling around with creating a wav file of a pure tone and observing what kind of loss of precision generates what kind of distortion and thought I'd share some results with you.
It is a common belief that computing upto the 7th degree of the Taylor series for a sine function is a good enough approximation for a sine function.
Wrong. You need alteast one more degree i.e. upto 9th degree to achieve a sine wave which has very little distortion.
Here's a screen shot of the FFT of a 500hz sine wave produced with the sine function computing only upto the 7th degree -
Attachments
percy said:
Hi,
FYI, have also a look here: http://www.fesb.hr/~mateljan/arta/
It works with 192 kHz soundcards as well. The build-in sine generator can do dual tones with adjustable ratio quite accurate. Attached a picture of a loop through measurement of my USB soundcard at 44.1 kHz.
😉
Attachments
- Status
- Not open for further replies.