What of math for bass-treble tone control design

Jump to Latest
fubar3

fubar3

Member
Joined 2011
#1
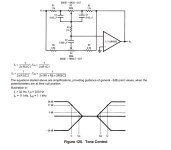
The free National Audio Book chapter 2.4 has schematics and component selection procedures for passive and active audio tone controls. I would like to automate the procedures so there is error checking and minimal tedious keyboard work. But the National examples do not report the results for 3db calculations.

The bass-treble example in LM4562 spec prints:-

// These are the different values for example in the LM4562 spec
// fL ≈ 32 Hz, fLB ≈ 320 Hz
// fH ≈ 11 kHz, fHB ≈ 1.1 kHz

But my script prints:-
// 31.83, 289.37, 8841.94, 869.70
// Minimum treble R4 pot 292000.0

So they diverge too much for treble values. I verified my calculations with the Digikey 3db filter app ... ok

It does not matter if these maths are done with 4-byte floats or 8-byte double precision. I wrote a small C program for testing. Most software languages depend upon standard C/C++ libraries so results should be consistent across applications.

Since the National Handbook is dated 1976, the math was probably done on an ancient minicomputer with unknown software quality.

Another concern is the high value pots, 100k to 500k, used for these controls. Would they be noisy for audio circuits?
 
#2
I would have to see the schematic and run a sim, but staying with the obvious, the hF turnover is suspect.

100k and 500k pots are way too high. Aim for 5k, and if you don’t mind paralleling the op amp you can go down to 1k or 2k, and there are several Vishay conductive plastic types that would suit. Depending on the type of tone circuit, the actual load which the op amp sees can be lower than expected, but the LM4562 can handle 400 Ohms at 10V swings quite well with about .001% THD or less. Sharing the load between more than one op amp lowers the harmonic distortion.
 
#3
I verified in 2021 that the LM4562 and National calculations are not correct. Yours are close, apart from the minimum treble pot, which is about 390k. Note that National said their equations were approximate. I get FL=31.8, FLB=289, otherwise same as you.

However don’t blame this on minicomputers ;-) I can assure you that the ones I was using in 1976 were accurate enough for this, even with 32-bit floating point.
 
  • Like
Reactions: JMFahey
#4
The National Handbook has a multistep procedure in chapter 2.4. You have to select a practical capacitor or pot after certain steps because the calculations only give abstract results. For example, the treble pot abstract value is 366000 which is satisfied by a 500k pot. After the design is complete, the calculations on the 4562 doc will reveal the 3db true frequencies. The example design was for 30hz and 10khz which was not realized.

Here is how they differ graphically.
differ1.png


here is other related link
https://www.digikey.ca/en/resources/online-conversion-calculators
 
#6
There are mysteries when doing design using the math in National Handbook..
  • Can the 500k treble pot be reduced to 100k like the bass pot?
  • Why not use 10k or 20k pots?
  • Document schematic does not match the given math

Good news.. The treble pot value is not required for the tone control calculations. Ergo, it can match the bass pot. But there is a constraint on the treble pot value (R3+R1+2*R5) which affects the "fHB" calculation. Then (2.14.17), with no evidence, multiplies this
constraint by 10 for the value of the treble pot. It looks like this:"R4 >= 10(R3+R1+2R5)". This is probably why many tone control examples have a large treble pot. My script does not do this.

I have modified the document math statements, seven step procedure, to normal form for computer processing. Then I used Lua to process the simple script which has no loops or branches .. just math statements which could be implemented in any language with a math library.

The document schematic does not match the math because the schematic capacitors have convenient substitutions which change the corner frequencies stated in the example design goal. Running the script
twice exposes the bug. Before running the second time, edit the overide values which will print the new frequencies.

-- Line 100: change ideal values to practical values
R1=11000 -- was 11111.11111
C1=0.05 -- was .04776 uf
R3=3700 -- was 3703 so insignificant difference
C3=.005 -- was .00429 uf
R5=R1
-- end change

-- second run of script....

--Example 2.14.2 Active Tone Control development--
--From the National Handbook--
R1= 11111.111111111
R2= 100000 bass pot
C1= 0.047746482927569 uf
R5= 11111.111111111
R3= 3703.7037037037
C3= 0.0042971834634812 uf
R4= 37037.037037037 ..treble pot minimum

Print abstract results for 2.14.13a on page 58, 2-45...
_fL= 33.333333333333 hz
_fLB= 300.0 hz
_Avb= 10.0 units
_fH= 10000.0 hz
_fHB= 1000.0 hz
_Avt= 10.0 units

Print results again after overide with practical value...
_fL= 31.830988618379 hz
_fLB= 289.37262380345 hz
_Avb= 10.090909090909 units
_fH= 8602.9698968592 hz
_fHB= 867.32939014657 hz
_Avt= 9.9189189189189 units
 

Attachments

#14
ejp said:
Wireless World 1952. https://www.thermionic.info/baxandall/Baxandall_NegativeFeedbackTone.pdf
Click to expand...
ejp said:
For the correct equations see Baxandall’s original paper.
Click to expand...
The original paper is conceptual. I don't understand it but that is ok because others have published a procedure which I expressed as a script to eliminate tedium. It is application, not concept.

I found no mistake in the Handbook except the concern about the treble pot high value. Actually, the treble pot value is arbitrary so it can be the same as the bass pot. It has no affect on the procedure results.
 
#16
ejp said:
The mistake is that the turnover frequencies they give don't agree with the equations and component values they give
Click to expand...
That is correct. I realized what happened after reading the document many times. The calculations usually give inconvenient values. They replaced them with .05 and .005 even before the procedure was completed. They should have highlighted and explained that inaccurate trick.
 
#17
Here is a fix for the tone control example in the National Semiconductor Audio Handbook 1977 or 1980..
Print results for 2.14.13a on page 58, 2-45...
R1= 11111.111111111 ..
R2= 100000 ..bass pot
R3= 3703.7037037037 ..
R4= 100000 ..treble pot = bass pot
R5= 11111.111111111 ..
C1= 0.047746482927569 ..uf
C3= 0.0042971834634812 ..uf
R4min= 37037.037037037 .. minimum treble pot
--
Avb= 10.0 ..units
fL= 33.333333333333 ..hz
fLB= 300.0 ..hz
Avt= 10.0 ..units
fH= 10000.0 ..hz
fHB= 1000.0 ..hz
Cheers..

-- file: rc100k.lua -- print bass-treble audio control tone resistors and caps -- -- 2024-jul-24 --[[ Description: Given National Semiconductor Audio Handbook 1977 or 1980, use a software script to reproduce design example 2.14.2 for Bass-Treble tone controls which needs +20dB gain, low corner = 30hz, upper = 10kHz. This script calculates component values. Resistor values have minimal impact on results. For example, R1 can be 11k instead of 11111.1k, R3 can be 3700. Capacitor values should be very close to the script result. For example, C3=.004297183uf, use .0043uf or 4300pf for that. The Handbook substituted 0.005uf which shifted the fH down by 1500hz. Take care when modifying results. For example, R1 depends upon gain and it affects all calculations that follow. Existing designs can be updated or evaluated with the script only if the original design goal is known. ]]-- MICRO = (1e6) -- for microfarad caps NANO = (1e9) -- for nanofarad caps PICO = (1e12) -- for picofarad caps PI2 = 2 * math.pi K = 1000 -- known values to achieve DESIGN GOAL Avb = 10 -- +20dB R2 = 100*K -- typical bass pot R4 = R2 -- treble pot same as bass pot fL = 30 -- required for lower 3db corner fH = 10*K -- required for upper corner -- declare unknowns fLB=0; fHB=0; R1=0; R3=0; R5=0; C1=0; C3=0 R1 = R2 / (Avb-1) R5 = R1 fLB = Avb*fL C1 = MICRO/(PI2 * fLB * R1) R3 = (R1 + 2*R5)/(Avb-1) --assuming Avt==Avb C3 = MICRO/(PI2 * fH * R3) -- these are Lua print statements, other languages may vary in format print("\n Print results for 2.14.13a on page 58, 2-45...") -- computed values can be rounded (maybe) -- R1=11*K; R5=R1 -- experiment -- C1=.05 -- experiment -- C3=.0043 -- experiment print("R1=", R1, "\t\t..") print("R2=", R2, "\t\t..bass pot") print("R3=", R3, "\t\t..") print("R4=", R4, "\t\t..treble pot = bass pot" ) print("R5=", R5, "\t\t..") print("C1=", C1, "..uf") print("C3=", C3, "..uf" ) print("R4min=", ( R3 + R1 + 2*R5), "\t.. minimum treble pot") print("--") print("Avb=", 1 + R2/R1, "\t\t..units" ) print("fL=", MICRO/(PI2 * R2 * C1), "\t..hz" ) print("fLB=", MICRO/(PI2 * R1 * C1), "\t\t..hz" ) print("Avt=", 1 + (R1 + 2*R5)/R3, "\t\t..units") print("fH=", MICRO/(PI2 * R3 * C3), "\t\t..hz") print("fHB=", MICRO/(PI2 * (R1+R3+2*R5)*C3), "\t\t..hz") print("Cheers..")
 
Last edited:
#18
fubar3 said:
The free National Audio Book chapter 2.4 has schematics and component selection procedures for passive and active audio tone controls. I would like to automate the procedures so there is error checking and minimal tedious keyboard work. But the National examples do not report the results for 3db calculations.

The bass-treble example in LM4562 spec prints:-

// These are the different values for example in the LM4562 spec
// fL ≈ 32 Hz, fLB ≈ 320 Hz
// fH ≈ 11 kHz, fHB ≈ 1.1 kHz

But my script prints:-
// 31.83, 289.37, 8841.94, 869.70
// Minimum treble R4 pot 292000.0

So they diverge too much for treble values. I verified my calculations with the Digikey 3db filter app ... ok

It does not matter if these maths are done with 4-byte floats or 8-byte double precision. I wrote a small C program for testing. Most software languages depend upon standard C/C++ libraries so results should be consistent across applications.

Since the National Handbook is dated 1976, the math was probably done on an ancient minicomputer with unknown software quality.

Another concern is the high value pots, 100k to 500k, used for these controls. Would they be noisy for audio circuits?
Click to expand...
Can you attach the schematic?
For the current standards 100k and 500k are not suitable - too much noise.
As LM4562 can drive low impedance loads you can try 2-5k pots.
 
#20
Hey @sherab
See post #5 above for Handbook downloads.

Here are results for 10k pots. The gain is reduced from 20dB to 15.5dB. Capacitors are bigger.
Here is a good page to read. See figure 5. Consider buying a PCB https://sound-au.com/articles/eq.htm

Based on 2.14.13a on page 58, 2-45...
results for 10k pots
R1= 2000.0 ..
R2= 10000 ..bass pot
R3= 1200.0 ..
R4= 10000 ..treble pot = bass pot
R5= 2000.0 ..
C1= 0.44209706414415 ..uf
C3= 0.013262911924325 ..uf
R4min= 7200.0 .. minimum treble pot
--
Avb= 6.0 ..uni ts
fL= 36.0 ..hz
fLB= 180.0 ..hz
Avt= 6.0 ..units
fH= 10000.0 ..hz
fHB= 1666.6666666667 ..hz
Cheers..
 
You must log in or register to reply here.
Top Bottom