Thanks David. The difference between the exponential and Le Cléac'h profile seems very slight.
Is there a horizontal part at the end of the curve for the Le Cléac'h profile?
A good pickup, thanks Bjørn.
The final data point was inadvertently omitted from the Lec profile curve. The corrected chart is attached.
I know you know this but for the benefit of others who may be interested, the reason why there is a slight difference and why the two profiles can never be exactly the same, as I mentioned earlier, is because the exponential profile is calculated assuming plane wavefront areas expanding exponentially, whereas the Le Cléac'h profile with T = 1 assumes curved "isophase" wavefronts expanding exponentially.
Matching a compression driver having a short exponential exit duct to a Le Cléac'h horn with T = 1 represents the best case scenario, and even then the match cannot be exact, for the reason given above. This is why I suggested simply making the throat entry angle of the horn equal to the exit angle of the compression driver duct - it should be good enough for all practical purposes.
Attachments
Just to state, for jmlc horns there is only one single opening angle for a given throat diameter, fc and T value assuming a spherical cap or even a planar wavefront at throat because in the first iteration the last added section inevitably determines the opening angle mathematically:
https://sphericalhorns.net/category/jmlc-horns/
If we talk about driver exit angle then we should take into account the length of the conical section. I mean a 3mm conical section with opening angle of 30 degrees, how relevant is it? If you have a driver with a too wide opening then just measure it first before modifying the horn math. There are several examples here how to ad an inlay to the driver making the opening angle more narrow. With modern 3D print technologies this should be no big issue.
If you want to change the horn math then you need a changing T value. For this I implemented the PETF algorithm some time ago (also negative values for Tadd are possible):
https://sphericalhorns.net/category/petf-horns/
What most here maybe have in mind is a true CE horn, so with a conical section or conical bell for a driver with wide opening angle and where the curvature to the exponential horn is equal the transition to an exponential section can take place. But this would compromise loading.
The rule of thumb is simply to avoid wide opening angle compression drivers for exponential horns or print an inlay. There are still so nicely designed drivers with an opening angle of almost zero when the pp almost ends up at throat exit. These drivers leave all possibilities to the horn designer.
https://sphericalhorns.net/category/jmlc-horns/
If we talk about driver exit angle then we should take into account the length of the conical section. I mean a 3mm conical section with opening angle of 30 degrees, how relevant is it? If you have a driver with a too wide opening then just measure it first before modifying the horn math. There are several examples here how to ad an inlay to the driver making the opening angle more narrow. With modern 3D print technologies this should be no big issue.
If you want to change the horn math then you need a changing T value. For this I implemented the PETF algorithm some time ago (also negative values for Tadd are possible):
https://sphericalhorns.net/category/petf-horns/
What most here maybe have in mind is a true CE horn, so with a conical section or conical bell for a driver with wide opening angle and where the curvature to the exponential horn is equal the transition to an exponential section can take place. But this would compromise loading.
The rule of thumb is simply to avoid wide opening angle compression drivers for exponential horns or print an inlay. There are still so nicely designed drivers with an opening angle of almost zero when the pp almost ends up at throat exit. These drivers leave all possibilities to the horn designer.
Maybe I should show a sketch to explain what I mean:
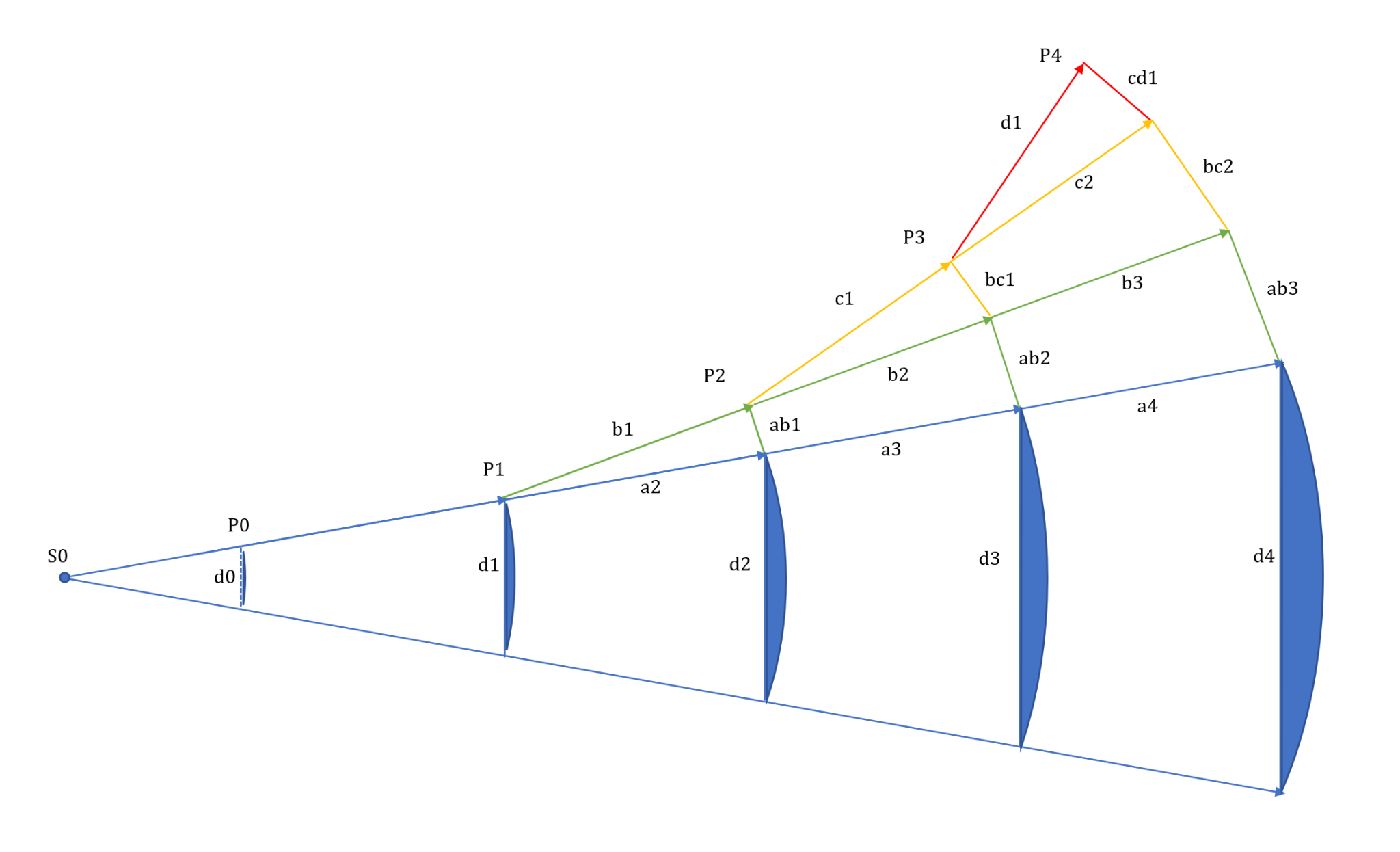
If we define a throat diameter d0 and want to assume a spherical cap as wavefront then imo the only coherent implementation of jmlc's algorithm is to optimize the opening angle, effectively by shifting S0, so that the surface area at P0 (throat) with an infinitesimal step size P0-P1 gives the correct surface area at P1 and diameter with a given fc and T value. There is only one single opening angle that fulfills the equations, and it can be optimized with a Newton optimization to minimize the error function sfa(exp)-sfa(P1)=0. But the resulting opening angle is dependent on the step size because all sections are conical but making the step size small we get a nice curved horn wall.
If we arrive at Px the center element is always a perfect radial element with origin S0 and all other elements combine coherently. It should be noted that ab3, bc2, cd1 as example are not straight lines as shown in sketch, they are indeed radial elements.
I like jmlc's algorithm very much, and it has similarities to an involute (https://en.wikipedia.org/wiki/Involute).
If we define a throat diameter d0 and want to assume a spherical cap as wavefront then imo the only coherent implementation of jmlc's algorithm is to optimize the opening angle, effectively by shifting S0, so that the surface area at P0 (throat) with an infinitesimal step size P0-P1 gives the correct surface area at P1 and diameter with a given fc and T value. There is only one single opening angle that fulfills the equations, and it can be optimized with a Newton optimization to minimize the error function sfa(exp)-sfa(P1)=0. But the resulting opening angle is dependent on the step size because all sections are conical but making the step size small we get a nice curved horn wall.
If we arrive at Px the center element is always a perfect radial element with origin S0 and all other elements combine coherently. It should be noted that ab3, bc2, cd1 as example are not straight lines as shown in sketch, they are indeed radial elements.
I like jmlc's algorithm very much, and it has similarities to an involute (https://en.wikipedia.org/wiki/Involute).
Speaking of which, how much difference in sweet spot size and spaciousness (due to reflected sound) might a horn with this directivity pattern exhibit compared to the AH425?
https://cdn.shopify.com/s/files/1/0...ot_2023-10-14_170306_480x480.png?v=1697317415
Larger coverage angles increase the "sweet spot" size, if by sweet spot you mean an area of similar frequency response.
AH425 polar map from:
https://kolbrek.hornspeakersystems.info/index.php/horns/bem
The horizontal dispersion of the ES-450 and AH425 both are ~100 degrees ~1kHz (similar reflected sound ), the AH425 more narrow in the 10kHz region (~45 degrees compared to ~66, less reflected sound).
The ES-450 vertical response probably is wider than the AH425 below 1kHz, and more narrow at 10kHz.
Art
Yes, what I mean. Thus it would seem that an exponential horn, like the ES450, while narrowing with rising frequencies still does give you more constant directivity coverage than the AH425.
I may be wrong but my hunch is that if going with a two rather than a three way design, unless nearly all of your source material is truly pristine, it's best not to risk choosing a horn which beams intensely even a bit lower than ~ 10kHz especially if choosing a highly transparent driver, such as
https://www.usspeaker.com/radian 760neoBepb-1.htm or
https://www.usspeaker.com/radian 951Bepb-1.htm
You are comparing two horns with similar flare rates and dispersion, neither have "constant directivity".
If you prefer to mask source material defects, it may be best not to choose to use horns, regardless of the frequency range they cover.